CoPheScan: Example with Hierarchical Priors

The hierarchical model is ideal when a large set of variants and phenotypes are available i.e., a phenome-wide association study with a set of variants which are previously known to have a functional role or have been implicated in a disease. Here we show how to use cophescan to infer hierarchical priors on a small test dataset.

library(cophescan)
library(dplyr)
library(ggplot2)

data("cophe_multi_trait_data")
trait_dat = cophe_multi_trait_data$summ_stat$Trait_1
str(trait_dat)
#> List of 8
#>  $ beta   : Named num [1:1000] -0.01369 0.01666 0.09057 -0.00571 -0.05606 ...
#>   ..- attr(*, "names")= chr [1:1000] "chr19-11173352" "chr19-11173626" "chr19-11173716" "chr19-11173807" ...
#>  $ varbeta: Named num [1:1000] 0.000516 0.000399 0.003124 0.000419 0.000473 ...
#>   ..- attr(*, "names")= chr [1:1000] "chr19-11173352" "chr19-11173626" "chr19-11173716" "chr19-11173807" ...
#>  $ z      : Named num [1:1000] -0.603 0.834 1.62 -0.279 -2.578 ...
#>   ..- attr(*, "names")= chr [1:1000] "chr19-11173352" "chr19-11173626" "chr19-11173716" "chr19-11173807" ...
#>  $ snp    : chr [1:1000] "chr19-11173352" "chr19-11173626" "chr19-11173716" "chr19-11173807" ...
#>  $ MAF    : Named num [1:1000] 0.2614 0.4871 0.0318 0.4046 0.3042 ...
#>   ..- attr(*, "names")= chr [1:1000] "chr19-11173352" "chr19-11173626" "chr19-11173716" "chr19-11173807" ...
#>  $ type   : chr "cc"
#>  $ N      : num 20000
#>  $ s      : num 0.5
querysnpid <- cophe_multi_trait_data$querysnpid
LD <- cophe_multi_trait_data$LD

Multi-trait analysis

The first step is preparing the input for the hierarchical model which are the log Bayes factors: lBF.Ha and lBF.Hc. We will use cophe.susie.lbf to extract Bayes factors estimated using SuSIE. Note: When there are no credible sets identified with SuSIE the function internally calculates lBF.Ha and lBF.Hc using the Approximate Bayes Factor method.

## Hide print messages from coloc
res.multi.lbf <- list()
for (trait_idx in seq_along(cophe_multi_trait_data$summ_stat)){
  querytrait_ss <- cophe_multi_trait_data$summ_stat[[trait_idx]]
  # Here LD is the same
  querytrait_ss$LD <- LD
  trait_variant_pair <- paste0('Trait', trait_idx, '_', querysnpid)
  res.multi.lbf[[trait_variant_pair]] <- cophe.susie.lbf(querytrait_ss, querysnpid = querysnpid, querytrait = paste0('Trait_', trait_idx))
}

res.multi.lbf.df = bind_rows(res.multi.lbf)

head(res.multi.lbf.df)
#>      lBF.Ha   lBF.Hc nsnps       querysnp querytrait           hit1
#> 1: 15.31003 11.95277  1000 chr19-11182353    Trait_1 chr19-11182353
#> 2: 16.43401 13.00673  1000 chr19-11182353    Trait_2 chr19-11182353
#> 3: 17.36744 13.13794  1000 chr19-11182353    Trait_3 chr19-11182353
#> 4: 14.45423 10.44441  1000 chr19-11182353    Trait_4 chr19-11182353
#> 5: 15.82635 12.54912  1000 chr19-11182353    Trait_5 chr19-11182353
#> 6: 16.23052 12.88257  1000 chr19-11182353    Trait_6 chr19-11182353
#>              hit2  typeBF idx1 idx2
#> 1: chr19-11182144 susieBF    1    1
#> 2: chr19-11183133 susieBF    1    1
#> 3: chr19-11189906 susieBF    1    1
#> 4: chr19-11182538 susieBF    1    1
#> 5: chr19-11176397 susieBF    1    1
#> 6: chr19-11182135 susieBF    1    1

Note:

The output of cophe.susie or cophe.single can also be used as input to the hierarchical model as it has all the fields required for the input. This would be useful when you would like to compare results from the fixed priors to those obtained from priors inferred using the hierarchical model. [Swap cophe.susie for cophe.susie.lbf above and instead of bind_rows do : res.multi.lbf.df = multitrait.simplify(res.multi.lbf)].
Use the for loop (as above) to run large datasets as storing all the coloc-structured data in a list is memory-intensive. This is also helpful in cases where there are multiple querysnps and different regions of the query traits have to be analysed

Run hierarchical model for priors

The input df for the multi.dat arguments should contain the following fields: “lBF.Ha”,“lBF.Hc” and “nsnps”.

Set the argument covar to TRUE to include covariates

covar=FALSE
covar_vec=rep(1, nrow(res.multi.lbf.df))
## Set covar to TRUE to include covariates, uncomment the following 2 lines 
# covar=TRUE
# covar_vec = cophe_multi_trait_data$covar_vec
cophe.hier.res <- run_metrop_priors(res.multi.lbf.df, avg_posterior=TRUE, avg_pik = TRUE, covar_vec = covar_vec, covar = covar, nits = 50000, thin = 5)
names(cophe.hier.res)
#> [1] "ll"            "parameters"    "avg.posterior" "avg.pik"      
#> [5] "data"          "nits"          "thin"

Note: Setting posterior or pik to TRUE is memory intensive for very large datasets

Diagnostics of the hierarchical model

Run 3-4 chains of the model and check if there is convergence of chains. Note: For large datasets run the chains separately and save them in individual .RData files. These can be loaded later for diagnostics.

cophe.hier.res.chain.list <- lapply(1:4, function(x) 
  run_metrop_priors(res.multi.lbf.df, avg_posterior=TRUE, avg_pik = TRUE, 
                    covar_vec = covar_vec, covar = covar, nits = 50000, thin = 5))

# Store user parameters
old_par <- par(no.readonly = TRUE)

# chain_colors <- c("#e63946c4", "#f1faee", "#a8dadc", "#457b9d" )
chain_colors <- c("#f4f1de", "#e07a5fb2", "#3d405bb2", "#81b29aa6")

layout(matrix(c(1, 2, 3, 4, 5, 5), ncol=2, byrow = TRUE), respect = TRUE, 
       heights = c(0.9, 0.9, 0.1))


matplot(sapply(cophe.hier.res.chain.list, function(x) x$ll), type = "l", 
        col = chain_colors, 
     main ="loglik", ylab = "ll", xlab = "Iteration", lty = 1)

y_ax <- c("alpha", "beta", "gamma")
num_pars <- ifelse(covar, 3, 2) 
for (idx in 1:num_pars) {
    matplot(sapply(cophe.hier.res.chain.list, function(x) x$parameters[idx, ]),
        type = "l", col = chain_colors,
        main = paste(y_ax[idx]), ylab = y_ax[idx], xlab = "Iteration", lty = 1
    )
}

if (!covar) {
    plot(1, type = "n", axes = FALSE, xlab = "", ylab = "")
}

par(mar=c(0, 0, 0, 0))
plot(1, type = "n", axes = FALSE, xlab = "", ylab = "")
legend("top", legend = paste("Chain", 1:4), col = chain_colors, lty = 1, lwd = 2, 
       horiz = TRUE, bty = "n")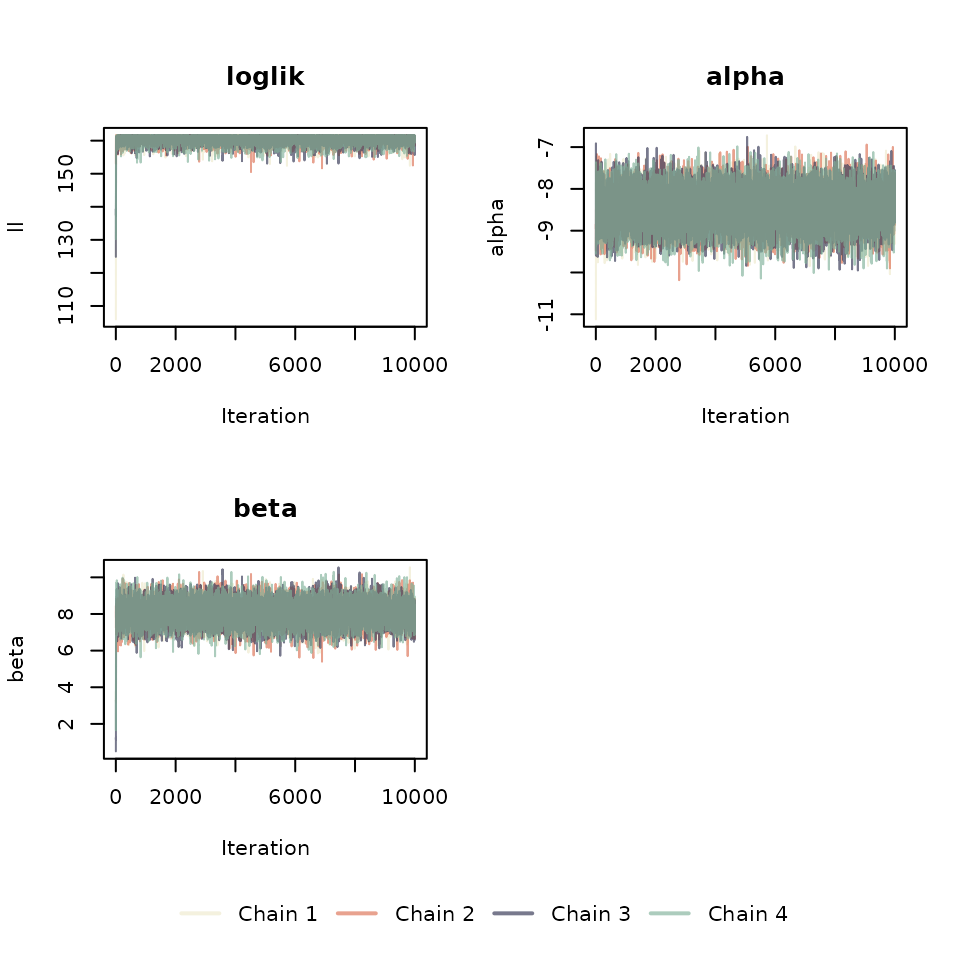


# Reset user parameters
par(old_par)

Prediction

cophe.hier.res.chain.list[[1]]$avg.posterior contains the posterior probabilities of the hypotheses : $H_n$, $H_a$ and $H_c$ for the queryvariant/querytrait pairs obtained from the hierarchical model. Here we use the first chain for prediction.

res.post.prob = cbind(cophe.hier.res.chain.list[[1]]$avg.posterior, cophe.hier.res$data)

We can use the cophe.hyp.predict function to predict the hypothesis given the posterior probabilities. The cophe.hyp.call column shows the predicted hypothesis for each query trait-query variant pair.

res.hier.predict <- cophe.hyp.predict(as.data.frame(res.post.prob ))
#> Hc.cutoff = 0.6
#> Hn.cutoff = 0.2
col_disp <- c( "PP.Hn", "PP.Ha", "PP.Hc", "nsnps", "querysnp", "querytrait",
               "typeBF",  "grp", "cophe.hyp.call")
knitr::kable(res.hier.predict[, col_disp], row.names = FALSE, digits=3)

PP.Hn	PP.Ha	PP.Hc	nsnps	querysnp	querytrait	typeBF	grp	cophe.hyp.call
0.773	0.099	0.128	1000	chr19-11182353	Trait_17	ABF	chr19-11182353_Trait_17	Hn
0.790	0.073	0.137	1000	chr19-11182353	Trait_18	ABF	chr19-11182353_Trait_18	Hn
0.798	0.083	0.119	1000	chr19-11182353	Trait_19	ABF	chr19-11182353_Trait_19	Hn
0.801	0.073	0.126	1000	chr19-11182353	Trait_20	ABF	chr19-11182353_Trait_20	Hn
0.694	0.058	0.248	1000	chr19-11182353	Trait_21	ABF	chr19-11182353_Trait_21	Hn
0.658	0.077	0.265	1000	chr19-11182353	Trait_22	ABF	chr19-11182353_Trait_22	Hn
0.790	0.081	0.129	1000	chr19-11182353	Trait_23	ABF	chr19-11182353_Trait_23	Hn
0.807	0.074	0.119	1000	chr19-11182353	Trait_24	ABF	chr19-11182353_Trait_24	Hn
0.000	0.999	0.000	1000	chr19-11182353	Trait_9	susieBF	chr19-11182353_Trait_9	Ha
0.001	0.999	0.000	1000	chr19-11182353	Trait_10	susieBF	chr19-11182353_Trait_10	Ha
0.000	1.000	0.000	1000	chr19-11182353	Trait_11	susieBF	chr19-11182353_Trait_11	Ha
0.002	0.998	0.000	1000	chr19-11182353	Trait_12	susieBF	chr19-11182353_Trait_12	Ha
0.001	0.999	0.000	1000	chr19-11182353	Trait_13	susieBF	chr19-11182353_Trait_13	Ha
0.000	0.999	0.000	1000	chr19-11182353	Trait_14	susieBF	chr19-11182353_Trait_14	Ha
0.000	1.000	0.000	1000	chr19-11182353	Trait_15	susieBF	chr19-11182353_Trait_15	Ha
0.000	1.000	0.000	1000	chr19-11182353	Trait_16	susieBF	chr19-11182353_Trait_16	Ha
0.000	0.011	0.989	1000	chr19-11182353	Trait_1	susieBF	chr19-11182353_Trait_1	Hc
0.000	0.012	0.988	1000	chr19-11182353	Trait_2	susieBF	chr19-11182353_Trait_2	Hc
0.000	0.025	0.975	1000	chr19-11182353	Trait_3	susieBF	chr19-11182353_Trait_3	Hc
0.000	0.020	0.979	1000	chr19-11182353	Trait_4	susieBF	chr19-11182353_Trait_4	Hc
0.000	0.010	0.990	1000	chr19-11182353	Trait_5	susieBF	chr19-11182353_Trait_5	Hc
0.000	0.011	0.989	1000	chr19-11182353	Trait_6	susieBF	chr19-11182353_Trait_6	Hc
0.000	0.008	0.992	1000	chr19-11182353	Trait_7	susieBF	chr19-11182353_Trait_7	Hc
0.000	0.013	0.987	1000	chr19-11182353	Trait_8	susieBF	chr19-11182353_Trait_8	Hc

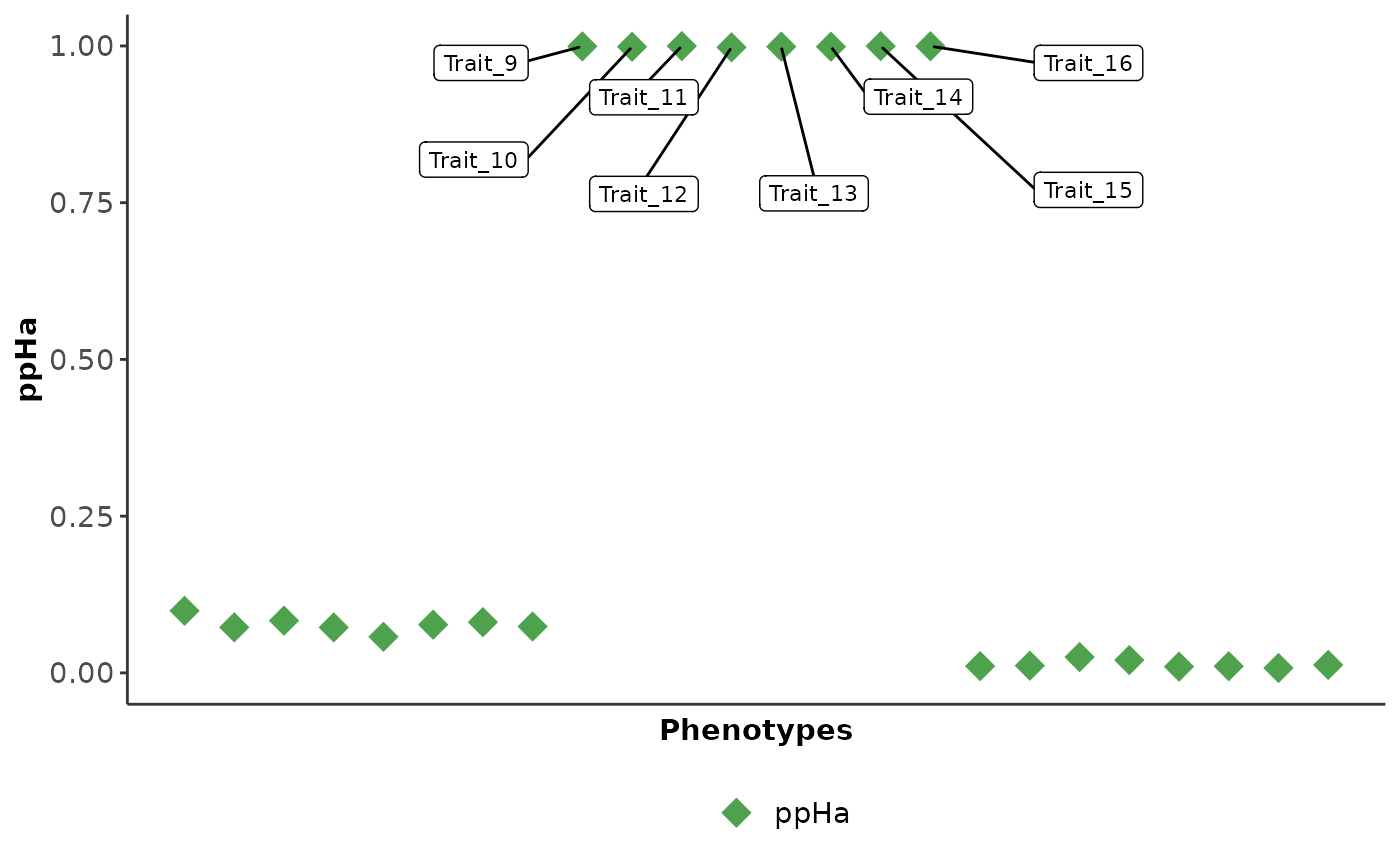
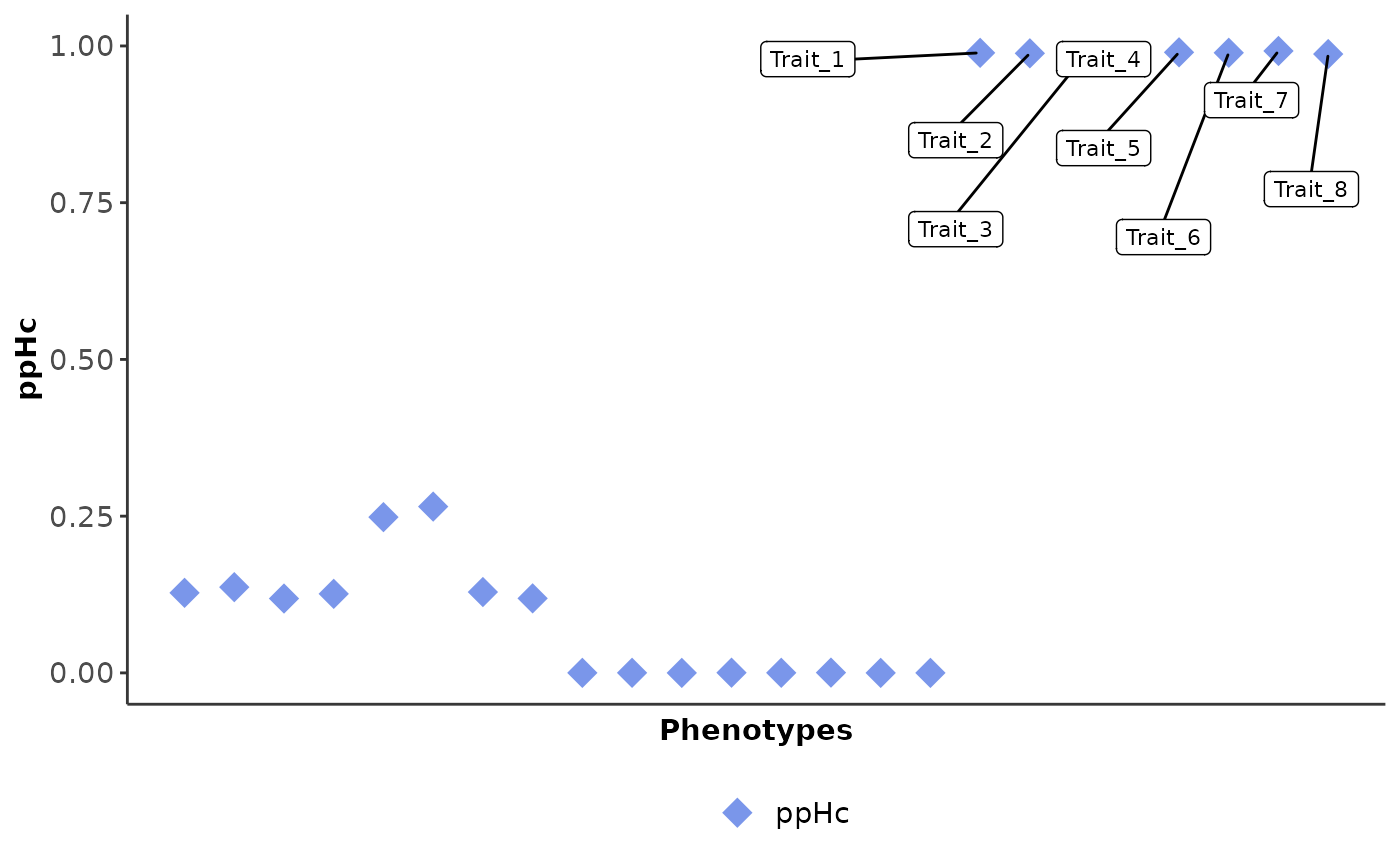
Visualisation

Use the cophe_plot function to return -log10(pval), ppHa and ppHc PheWAS plots from the cophescan output.

res.plots = cophe_plot(res.hier.predict, traits.dat = cophe_multi_trait_data$summ_stat, querysnpid = querysnpid, query_trait_names = paste0('Trait_', 1:24))

# if (!require(ggpubr)) {
  # install.packages("ggpubr") 
# }
# ggpubr::ggarrange(res.plots$pval, res.plots$ppHa, res.plots$ppHc, ncol = 2, 
#                 nrow = 2)

Note: For large datasets, it’s not feasible to input all coloc-structured data into “traits.dat” at once. Instead, use a loop and run the “get_beta” function over all the trait-variant pairs, and provide the resulting data frame (after binding the rows) as the “beta_p” argument in cophe_plot:

# beta_p_list <- lapply(seq_along(cophe_multi_trait_data$summ_stat),  function(x) get_beta(list(cophe_multi_trait_data$summ_stat[[x]]), querysnpid, names(cophe_multi_trait_data$summ_stat)[x]))
# ### the datsets need not be in a list as in cophe_multi_trait_data$summ_stat and can be stored independently.
# beta_p_df = bind_rows(beta_p_list)
# ### Make sure the query trait names in beta_p_df are the same as in res.hier.predict
# res.plots = cophe_plot(res.hier.predict,  querysnpid = querysnpid, query_trait_names = beta_p_df$querytrait, beta_p = beta_p_df)

Ichcha Manipur

2024-06-11

Multi-trait analysis

Run hierarchical model for priors

Diagnostics of the hierarchical model

Prediction

Visualisation